Commuting matrices

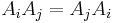In linear algebra, a set of matrices $A_1,\ldots,A_k$ is said to commute if they commute pairwise, meaning $A_iA_j = A_jA_i$ for every pair i, j (equivalently, the commutator vanishes: $[A_i,A_j]$ ; more abstractly, if the algebra they generate is an abelian Lie algebra).

Properties

Commuting matrices over an algebraically closed field are simultaneously triangularizable; indeed, over the complex numbers they are unitarily simultaneously triangularizable. Further, if the matrices 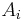$A_i$ have eigenvalues 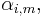$\alpha_{i,m},$ then a simultaneous eigenbasis can be chosen so that the eigenvalues of a polynomial in the commuting matrices is the polynomial in the eigenvalues. 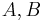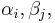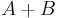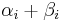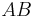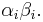For example, for two commuting matrices $A,B$ with eigenvalues $\alpha_i, \beta_j,$ one can order the eigenvalues and choose the eigenbasis such that the eigenvalues of $A%2BB$ are $\alpha_i %2B \beta_i$ and the eigenvalues for $AB$ are $\alpha_i\beta_i.$ This was proven by Frobenius, with the two-matrix case proven in 1878, later generalized by him to any finite set of commuting matrices.

This is generalized by Lie's theorem, which shows that any representation of a solvable Lie algebra is simultaneously upper triangularizable, the case of commuting matrices being the abelian Lie algebra case, abelian being a fortiori solvable.

History

References given in (Drazin 1951).

The notion of commuting matrices was introduced by Cauchy in his Memoir on the theory of matrices, which also provided the first axiomatization of matrices. The first significant results proved on them was the above result of Frobenius in 1878.

References

Drazin, M. (1951), "Some Generalizations of Matrix Commutativity", Proceedings of the London Mathematical Society, 3 1 (1): 222–231, doi:10.1112/plms/s3-1.1.222